New Page 1

　　　　　　　　　　　　　　　　　（理工农医类）参考答案

　　一、选择题(本题考查基本知识和基本运算)

　　　　1.C 　　　2.B 　　　3.C 　　　4.B 　　　5.D

　　　　6.D 　　　7.B 　　　8.C 　　　9.A 　　　10.D

　　　11.B 　　 12.C 　　 13.A 　　 14.D 　　 15.A

　　二、填空题(本题考查基本知识和基本运算)

　　三、解答题

　　　21.本小题主要考查复数基本概念和几何意义,以及运算能力.

　　　　解:设Z₁,Z₃对应的复数分别为z₁,z₃,依题设得

　　　　　　　　
　　　　　　　　　

　　22.本小题主要考查三角恒等式和运算能力.

　　　　解：　原式＝1/2(1－cos40°)＋1/2(1＋cos100°）＋sin20°cos50°

　　　　　　　　　＝1＋1/2(cos100°－cos40°)＋1/2(sin70°－sin30°)

　　　　　　　　　＝3/4－sin70°sin30°＋1/2sin70°

　　　　　　　　　＝3/4

　　23.本小题主要考查空间线面关系、圆柱性质、空间想象能力和逻辑推理能力.

　　　　(1)证明:根据圆柱性质,DA⊥平面ABE.

　　　　∴EB平面ABE

　　　　∴DA⊥EB.

　　　　∵AB是圆柱底面的直径,点E在圆周上,

　　　　∴AE⊥EB,又AE∩AD=A,

　　　　故得EB⊥平面DAE.

　　　　∴DF

平面DAE

　　　　∴EB⊥AF.

　　　　又AF⊥DE,且EB∩DE=E,

　　　　故得AF⊥平面DEB.
　　
　　　　∵DB

平面DEB

　　　　∴AF⊥DB.

　　(2)解:过点E作EH⊥AB,H是垂足,连结DH.根据圆柱性质,平面ABCD⊥平面ABE,AB是交线.且EH平面ABE,

　　　　所以EH⊥平面ABCD.

　　　　又DH平面ABCD,所以DH是ED在平面ABCD上的射影,从而∠EDH是DE与平面ABCD所成的角.

　　　　设圆柱的底面半径为R,则DA=AB=2R,于是

　　　　V圆柱=2πR³,

　　　　由V圆柱:DA＝BE=3π,得EH=R,可知H是圆柱底面的圆心,

　　　　AH=R,

　　　　　　

　　24.本小题主要考查运用所学数学知识和方法解决实际问题的能力,以及函数的概念、方程和不等式

　　　的解法等基础知识和方法.

　　　解:(1)依题设有

　　　　　　

　　　　　　　　 ②　0≤t ≤

　　　　　　　

　　25.本小题主要考查等比数列、对数、不等式等基础知识,考查推理能力以及分析问题和解决问题的

　　　能力.

　　　　　　(1)证明：设{a_n}的公比为q，由题设a₁＞0，q＞0.

　　　　　　　(i)当q＝1时，S_n＝na₁，从而

　　　　　　　　S_n－S_n+2－S_n+1²

　　　　　　　　＝na₁－(n＋2)a₁－(n＋1)2a₁²

　　　　　　　　＝－a₁²＜0

　　　　　　　(ii)当q≠1时，S_n＝a₁(1－q_n)/(1－q)，从而　

　　　　　　　　S_n－S_n+2－S_n+1²　

　　　　　　　　＝[na₁²·(1－q_n)(1－q_n+2)]/a₁²(1－q_n+1)²/(1－q)²

　　　　　　　　=－a₁²q_n＜0

　　　　　　　　由(i)和(ii)得Sn－Sn+2＜S_n+1²，根据对数函数的单调性，知

　　　　　　　　lg(S_n－S_n+2)＜lgS_n+1²,

　　　　　　　　即(lgS_n＋lgS_n+2)/2＜lgS_n+1,

　　　　　　　(2)解：不存在：

　　　　　　　　证明一要使

　　　　　　　　lg(S_n－c)＋lg(S_n+2－c)/2＝lg(S_n+1－c)，成立，则有

	(S_n－c)(S_n+2－c)＝(S_n+1－c)²　　　　　　①
	S_n－c＞0　　　　　　　　　　　　　　　②

　　　　　　　　分两种情况考虑

　　　　　　　当q＝1，时　(Sn－c)(Sn+2－c)－(Sn+1－c)2

　　　　　　　　　　　　　＝(na₁－c)[(n＋2)a₁－c]－[(n＋1)a₁－c]²

　　　　　　　　　　　　　=－a₁²＜0

　　　　　　　可知,不满足条件①,即不存在常数c>0,使结论成立.

　　　　　　　(ii)当q≠1时,若条件①成立,因为

　　　　　　　　　(S_n-c)(S_n+2-c)-(S_n+1-c)²

　　　　　　　　　＝[a₁(1－q_n)/(1－q)－c][a₁(1－q_n+2)/(1－q)－c]－[a₁(1－q_n+1)/(1－q)－c]²

　　　　　　　　　＝－a₁q_n[a₁－c(1－q)]，

　　　　　　　此时,因为c>0,a₁>0,所以0<q<1.

　　　　　　　当0＜q＜1时，S_n－a₁/(1－q)＝a₁q_n/(1－q)＜0，不满足条件②，即不存在常数c>0，使结

　　　　　　　论成立．

　　　　　　　综合(i)、(ii),同时满足条件①、②的常数c>0不存在,即不存在常数c>0,使

　　　　　　　　　[lg(S_n－c)＋lg(S_n+2－c)]/2＝lg(S_n+1－c)

　　　　　　　证法二:用反证法,假设存在常数c>0,使

　　　　　　　则有

　　　　　　　由④得
　　　　　　　　　
　　　　　　　　　S_nS_n+2-S_2n+1=c(S_n+S_n+2-2S_n+1).⑤
　
　　　　　　　根据平均值不等式及①、②、③、④知

　　　　　　　S_n+S_n+2-2S_n+1

　　　　　　　=(S_n-c)+(S_n+2-c)-2(S_n+1-c)

　　　　　　　因为c>0,故⑤式右端非负,而由(1)知,⑤式左端小于零,矛盾.故不存在常数c>0,使

　　26.本小题主要考查直线、椭圆的方程和性质,曲线与方程的关系,轨迹的概念和求法,利用方程判

　　　　定曲线的性质等解析几何的基本思想和综合运用知识的能力.

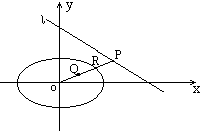
　　　　　　　　　　　　　 sx26.gif (839 bytes)

　　　　解法一：由题设知点Q不在原点.设P、R、Q的坐标分别为(x_{_p},y_{_p}),(x_{_R},y_{_R}),其中x,y不同时

　　　　　　　　为零.

　　　　　　　　当点P不在y轴上时,由于点R在椭圆上及点O、Q、R共线,得方程组

	x_R²/24＋y_R²/16＝1
	y_R/x_R＝y/x

　　　　　　　　　　解得

	x_R²＝48x²/(2x²＋3y²)　　　　①
	y_R²＝48y²/(2x²＋3y²)　　　　②

　　　　　　　　　　由于点P在直线l上及点O、Q、P共线，得方程

	x_P/12＋y_P/18＝1
	y_P/x_P＝y/x

　　　　　　　　　　解得　　　　　　　
　　　　　　　　　　
　　
　　　　解法二：由题设知点Q不在原点.设P,R,Q的坐标分别为(x_p,y_p),(x_R,y_R),(x,y),其中x,y不同时

　　　　　　　　　为零.

　　　　　　　　设OP与x轴正方向的夹角为α,则有

　　　　　　　　x_p=│OP│cosα,y_p=│OP│sinα;

　　　　　　　　x_R=│OR│cosα,y_R=│OR│sinα;

　　　　　　　　x=│OQ│cosα,y=│OQ│sinα;

　　　　　　　　由上式及题设|OQ|·|OP|＝|OR|²，得

	x_p＝\|OP\|/\|OQ\|x　　　　①
	y_p＝\|OP\|/\|OQ\|y　　　　②

	x_R²＝\|OP\|/\|OQ\|x²　　　 ③
	y_R²＝\|OP\|/\|OQ\|y²　　　 ④

　　　　　　　　由点P在直线l上，点R在椭圆上，得方程组

	x_P/12＋y_P/18＝1　　 ⑤
	x_R²/24＋y_R²/16＝1　　 ⑥

　　　　　　　　将①,②,③,④代入⑤,⑥,整理得点Q的轨迹方程为

　　　　　　　　　　(x－1)²/(5/2)＋(y－1)²/(5/3)＝1（其中x、y不同时为零）

　　　　　　　　与x轴平行的椭圆、去掉坐标原点.